引言
暴力搜索法(又称 穷举搜索,在计算机科学中也称生成与测试)是一种“简单粗暴地”处理问题的方法,通过枚举所有的可能并判断是否符合题意,以得出答案
但有时候直接枚举会带来问题:枚举量过大而存在大量不必要的枚举,导致算法时间复杂度过大(太低效了)。有没有更好的方法呢?
回溯法(backtracking) 是暴力搜索法的一种,可在递归构造中把搜索和检查有机地结合起来,从而减小枚举量
让我们通过几道经典的题目来感受一下回溯法的魅力吧~
八皇后问题
可以说是最经典的题目之一了。甚至常被作为“判断有没有学过回溯法”的依据 (刘老师如是说)
如何能够在8×8的国际象棋棋盘上放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后?为了达到此目的,任两个皇后都不能处于同一条横行、纵行或斜线上。
八皇后问题可以推广为更一般的n皇后摆放问题:这时棋盘的大小变为n×n,而皇后个数也变成n。当且仅当n = 1或n ≥ 4时问题有解。
——From 维基百科·八皇后问题
而我们要解决的,正是推广后的n皇后问题。但为了方便描述,下面的分析还是以八皇后问题为例
思路一:组合生成
枚举出所有可能的棋局,再来判断是否符合题目要求。
问题可以转换为:从 $ 8 \times 8 = 64 $ 个格子里选出 $8$ 个(即组合生成),保证任两个格子都不能处于同一条横行、纵行或斜线上
根据排列组合,我们知道共有$ C_{64}^{8} = 4.426 \times 10^9 $种方案,显然是太复杂了。
思路二:全排列生成
稍加思考,我们可以改进策略:恰好每行每列各选一个格子,保证任两个格子都在同一斜线上。如此转化为全排列生成的问题,方案数降为$ 8! = 40320 $种,肉眼可见的效率提升啊(笑)
我们可以用C[x]表示第x行皇后的列编号。难点之一是如何判断皇后间是否斜向攻击。
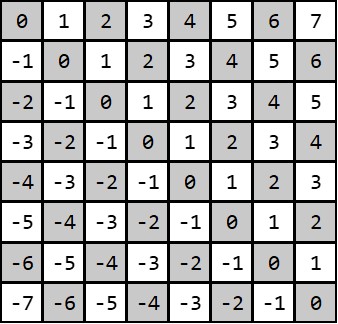
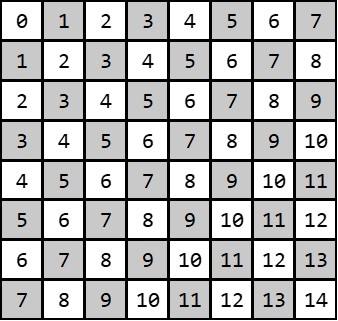
把棋盘看作一个以左上角为原点、往下为x轴、往右为y轴的平面直角坐标系,于是棋盘的主对角线就是 $ y = x $ ,于是对于格子$ (x,y) $, $ y-x $ 的值就标识了主对角线(确保你理解了这一点!)。同理,副对角线为 $ y = -x $ , $ x+y $ 的值标记了副对角线。如下图所示:
回溯法
接下来,就要用到回溯法了:
所谓回溯(backtracking),就是指在递归求解问题时,如果当前步骤没有合法选择,则函数返回上一级递归调用
简单来说,就是把问题分成若干个步骤递归求解,当某一步不合题意时停止,返回上一步。这样可以大大减少运算量
来看看代码吧~
普通回溯法
nqueens_1.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
// n皇后问题:在n*n棋盘上放置n个皇后,使得它们互不攻击,找出所有解
#include <iostream>
#include <cstring>
using namespace std;
int C[50], tot = 0, n = 8, nc = 0;
// C[x]表示第x行皇后的列编号
void search(int cur)
{
nc++; // 递归次数
if (cur == n) tot++; // 递归边界。只要走到了这里,所有皇后必然不冲突
// if (cur == n) // 打印解
// {
// printf("解%d: ", tot);
// for (int i = 0; i < n; i++)
// printf("(%d,%d) ", i, C[i]);
// printf("\n");
// }
else for (int i = 0; i < n; i++)
{
int ok = 1;
C[cur] = i; // 尝试把第cur行的皇后放在第i列
for (int j = 0; j < cur; j++) // 检查是否和前面的皇后冲突
// 对于(x,y),y-x值为主对角线,y+x值为副对角线
if (C[cur] == C[j] || cur-C[cur] == j-C[j] || cur+C[cur] == j+C[j])
{ ok = 0; break; }
if (ok) search(cur+1); // 如果合法,则继续递归
}
}
int main()
{
while (cin >> n)
{
search(0);
cout << "解的个数: " << tot << endl;
cout << "递归次数: " << nc << endl;
nc = 0; tot = 0; memset(C, 0, sizeof(C));
}
return 0;
}
|
这样就解决了这个问题。结点数似乎很难再减少了,但效率还可以提高!
优化的回溯法
利用二维数组vis[2][]存储状态,来直接判断当前尝试的皇后所在的列和两个对角线是否已有其他皇后。因为$ y-x $可能为负,存储时要加上n(数组下标不能为负)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int C[50], vis[3][50], tot = 0, n = 8, nc = 0;
// 利用二维数组vis[2][]直接判断当前尝试的皇后所在的列和两个对角线是否已有其他皇后
void search(int cur)
{
int i;
nc++;
if (cur == n) tot++;
// if(cur == n)
// {
// printf("解%d: ", tot);
// for (int i = 0; i < n; i++)
// printf("(%d,%d) ", i, C[i]);
// printf("\n");
// }
else for(i = 0; i < n; i++)
{
if (!vis[0][i] && !vis[1][cur+i] && !vis[2][cur-i+n])
{
C[cur] = i; // 如果不用打印解,整个C数组都可以省略
vis[0][i] = vis[1][cur+i] = vis[2][cur-i+n] = 1; // 访问标记
search(cur+1);
vis[0][i] = vis[1][cur+i] = vis[2][cur-i+n] = 0; // 及时改回来!
}
}
}
int main()
{
while (cin >> n)
{
memset(vis, 0, sizeof(vis));
search(0);
cout << "解的个数: " << tot << endl;
cout << "递归次数: " << nc << endl;
tot = 0; nc = 0;
}
return 0;
}
|
注意访问标记的设置,即对辅助全局变量(数组vis)的修改,并且在结束访问后即使修改回来!
生成 - 测试法
作为比较,我们看看生成 - 测试法的效率如何
nqueens_3.cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
#include <iostream>
#include <cstring>
using namespace std;
int C[50], tot = 0, n = 8;
long long nc = 0;
// 先生成棋面,再判断
void search(int cur)
{
int i, j;
nc++;
if(cur == n)
{
for(i = 0; i < n; i++)
for(j = i+1; j < n; j++)
if(C[i] == C[j] || i-C[i] == j-C[j] || i+C[i] == j+C[j]) return;
tot++;
}
else for(i = 0; i < n; i++)
{
C[cur] = i;
search(cur+1);
}
}
int main()
{
while (cin >> n)
{
memset(C, 0, sizeof(C));
search(0);
cout << "解的个数: " << tot << endl;
cout << "递归次数: " << nc << endl;
tot = 0; nc = 0;
}
return 0;
}
|
我们来对比一下这几个程序的效率(测试设备CPU为i9-12900H)
递归次数
| 程序 \ n |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| nqueen_1.cpp |
2057 |
8394 |
35539 |
166926 |
856189 |
4674890 |
27358553 |
171129072 |
1141190303 |
| nqueen_2.cpp |
2057 |
8394 |
35539 |
166926 |
856189 |
4674890 |
27358553 |
171129072 |
1141190303 |
| nqueen_3.cpp |
19173961 |
435848050 |
11111111111 |
- |
- |
- |
- |
- |
- |
耗时(单位:s)
| 程序 \ n |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| nqueen_1.cpp |
0.001 |
0.002 |
0.006 |
0.028 |
0.147 |
0.877 |
5.582 |
38.462 |
284.097 |
| nqueen_2.cpp |
0.001 |
0.002 |
0.003 |
0.012 |
0.056 |
0.298 |
1.828 |
11.761 |
80.594 |
| nqueen_3.cpp |
0.124 |
3.2 |
91.716 |
- |
- |
- |
- |
- |
- |
当 $ n \leq 13 $ 时,回溯法和优化后的回溯法有不错的效率;当 $ n > 13 $ 时,优化后回溯法的效率明显更高
而生成-测试法的复杂度明显高得多,$ n = 10 $ 时耗时长达约一分半,递归次数也远超出INT类型的范围
Python代码
nqueen.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
def print_solve():
global tot, n, C
print(f"解:{tot}")
for i in range(n):
print(f"({i},{C[i]})", end=" ")
print()
def search(cur):
global C, vis, tot, n, nc
nc += 1
if cur == n:
tot += 1
if cur == n:
print_solve()
else:
for i in range(n):
if vis[0][i] == 0 and vis[1][cur+i] == 0 and vis[2][cur-i+n] == 0:
C[cur] = i
vis[0][i] = 1
vis[1][cur+i] = 1
vis[2][cur-i+n] = 1
search(cur+1)
vis[0][i] = 0
vis[1][cur+i] = 0
vis[2][cur-i+n] = 0
while 1:
C = [0]*30
vis = [[0]*30 for _ in range(3)]
tot = 0
n = 0
nc = 0
try:
n = int(input())
except:
print("error.")
search(0)
print(f"解的个数:{tot}")
print(f"递归次数:{nc}")
|
效率飞一般的提升!快去试试吧!
(To be continue…)
更新了一些数学公式(终于会用Katex了)
——2023/01/12

附录
参考文献
[1]刘汝佳《算法竞赛入门经典(第2版)》
[2]维基百科·暴力搜索
[3]维基百科·回溯法
[4]维基百科·八皇后问题
版权信息
本文原载于https://blog-allenwu233.netlify.app/,复制请保留原文出处
![]()
![]()
![]()