有人说贪心算法是最简单的算法,原因很简单:你我其实都很贪,根本不用学就知道怎么贪。有人说贪心算法是最复杂的算法,原因也很简单:这世上会贪的人太多了,那轮到你我的份?
——By CSDN@lloil
贪心算法简介
什么是贪心算法
贪心算法(greedy algorithm,又称贪婪算法) 是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择。
——By 百度百科·贪心算法
基本要素
1.贪心选择性质
一个问题的整体最优解可通过一系列局部的最优解的选择,即贪心选择达到,并且每次的选择可以依赖以前作出的选择,但不依赖于后面要作出的选择。这就是贪心选择性质。
对于一个具体问题,要确定它是否具有贪心选择性质,必须证明每一步所作的贪心选择最终导致问题的整体最优解
2.最优子结构性质
当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。
问题的最优子结构性质是该问题可用贪心法求解的关键所在。在实际应用中,至于什么问题具有什么样的贪心选择性质是不确定的,需要具体问题具体分析
基本思路
从问题的某一个初始解出发逐步逼近给定的目标,以尽可能快的地求得更好的解。
当达到算法中的某一步不能再继续前进时,算法停止。
该算法存在问题:
- 不能保证求得的最后解是最佳的;
- 一般用来求最大或最小解问题;
- 只能求满足某些约束条件的可行解的范围。
实现该算法的过程:
从问题的某一初始解出发:
|
|
一道简单的例题
题目如下
原题:拼座椅
题目描述
上课的时候总有一些同学和前后左右的人交头接耳,这是令小学班主任十分头疼的一件事情。不过,班主任小雪发现了一些有趣的现象,当同学们的座次确定下来之后,只有有限的D对同学上课时会交头接耳。
同学们在教室中坐成了 M 行 N 列,坐在第 i 行第 j 列的同学的位置是(i,j)(i,j),为了方便同学们进出,在教室中设置了 K 条横向的通道,LL 条纵向的通道。于是,聪明的小雪想到了一个办法,或许可以减少上课时学生交头接耳的问题:她打算重新摆放桌椅,改变同学们桌椅间通道的位置,因为如果一条通道隔开了两个会交头接耳的同学,那么他们就不会交头接耳了。
请你帮忙给小雪编写一个程序,给出最好的通道划分方案。在该方案下,上课时交头接耳的学生对数最少。
输入描述:
第一行,有 5 各用空格隔开的整数,分别是 M,N,K,L,D(2 ≤ N,M ≤ 1000,0 ≤ K < M,0 ≤ L < N,D ≤ 2000)。
接下来 D 行,每行有 4 个用空格隔开的整数,第 i 行的 4 个整数 X_i,Y_i,P_i,Q_i,表示坐在位置 (X_i, Y_i) 与 (P_i, Q_i) 的两个同学会交头接耳(输入保证他们前后相邻或者左右相邻)。 输入数据保证最优方案的唯一性。
输出描述
共两行:
第一行包含 K 个整数, a_1 a_2 … a_k, 表示第 a_1 行和 a_1 + 1 行之间、第 a_2 行和第 a_2 + 1 行之间、…、第 a_k 行和第 a_k + 1 行之间要开辟通道,其中 a_i < a_i + 1 ,每两个整数之间用空格隔开(行尾没有空格)。
第二行包含 L 个整数, b_1 b_2 … b_k,表示第 b_1 列和 b_1 + 1 行之间、第 b_2 行和第 b_2 + 1 行之间、…、第 b_l 行和第 b_l + 1 行之间要开辟通道,其中 b_l < b_l + 1,每两个整数之间用空格隔开(行尾没有空格)。
示例
输入
1 2 3 44 5 1 2 3 4 2 4 3 2 3 3 3 2 5 2 4输出
1 22 2 4
说明
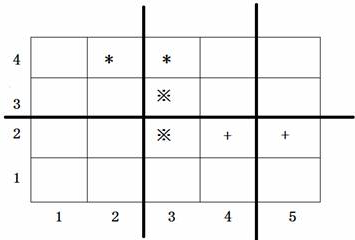
上图中用符号*、※、+ 标出了3对会交头接耳的学生的位置,图中3条粗线的位置表示通道,图示的通道划分方案是唯一的最佳方案。
题目分析
这是一道典型的贪心算法题。要满足交头接耳的学生对数最少,只需选择能分开学生对数最多的行和列即可。
有人把这道题比喻成切虫子:有若干条长度为 2 的 虫子,怎么切才能使切死的虫子数最多(莉格露表示强烈谴责)
然而即便是这么简单的题,也有不少 难点/陷阱
- 注意输出:行尾没有空格
- 升序输出
- 重点(针对 C 语言):如何在一个数组中求值前 k 大的值(不改变下标)
- 冒泡排序
关于第三点的说明
如:求int arr[] = {1, 7, 6, 8, 32}中第一大的值、第二大的值、第三大的值……
方法:
- 在外面定义
int max_num = 0,然后遍历数组,比max_num大的值就将它赋给max_num,即获取最大值- 再次遍历数组,将第一个数组值等于
max_num的值置为-1,这样下一次求得的是第二大的值- 重复步骤1、2,直至求得所有待求值
理论成立,上 ~ 代 ~ 码 ~
源代码
C
|
|
Python
参考:@comter
Python 的map()、count()和sort()等函数可以省不少功夫
这就是我更喜欢 Python 的原因之一(笑)
|
|
才二十几行代码就解决了 C 七十几行代码才解决的问题
总结
算法不愧是编程的灵魂……
这才是编程的浪漫啊!(因解题时间过长理智丧失ing…)

参考文献
To Be Continue…
关于贪心算法,我只是学了点皮毛而已,以后还会在这里更新更加deep♂dark的用法