引言
在印度,有这样一个古老的传说。在世界中心贝拿勒斯的圣庙里,一块黄铜板上插着3根宝石针。印度教的主神梵天在创造世界的时候,在其中一根针上从下到上地穿好了由大到小的64片金盘,这就是所谓的汉诺塔(Tower of Hanoi)。不论白天黑夜,总有一个僧侣在按照下面的法则移动这些金盘到另一根针上:一次只移动一片,而且小片必在大片上面。当所有的金盘都从梵天穿好的那根针上移动到第三根针上时,世界就将在一声霹雳中消灭,梵塔、庙宇和众生都将同归于尽……
分析问题
什么是汉诺塔
总结如下:
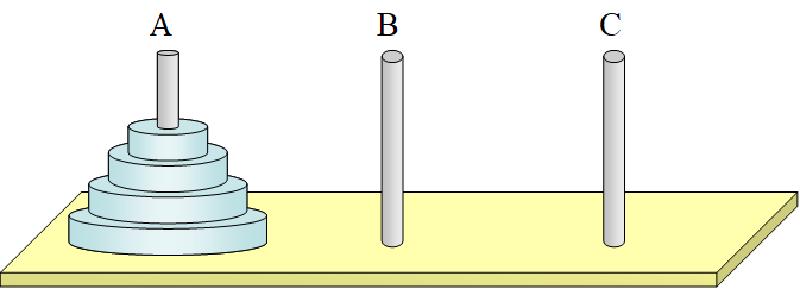
有 A, B, C 三根柱子,A 柱上有 n(n > 1) 个金盘,金盘的尺寸由下到上依次变小。每次只能移动一片金盘,且大金盘不能位于小金盘之上,使得所有金盘都移动到 C 柱。
问:如何移?最少要移动多少次?
一个最简单的例子
当 n = 1 时,只需1步就能解决:A-->C
( A-->C 表示把 A 柱最上面的一个金盘移动到 C 柱,下同)
一个很简单的例子
当 n = 2 时,只需3步:
一个简单的例子
当 n = 3 时,用一张图来解决:
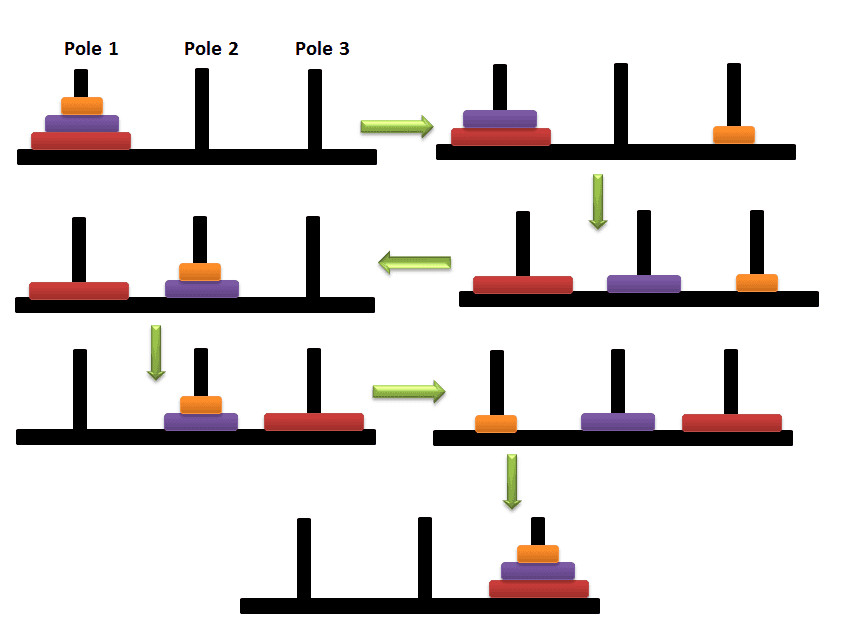 用语言表述如下:
用语言表述如下:
1
2
3
4
5
6
7
|
A-->C
A-->B
C-->B
A-->C
B-->A
B-->C
A-->C
|
共需7步
扩展到 n
当 n = 4, 5, 6 甚至 20 时,又该怎么办呢?
这个问题看起来很复杂,其实是有规律可循的
根据数学方法计算得出,移动 n 层的汉诺塔所需次数为
关于具体证明的讨论就不属于本文的范畴了
分析算法
可以用递归的思想来解决
将n个金盘从A柱移动到C柱可分解为以下三个步骤:
- 先将 A 柱上的 n-1 个金盘借助于 C 柱移到 B 柱上(把 C 看作临时柱)
- 这一步又可分解为以下三步:
- 将 A 柱上的 n-2 个金盘借助于 B 柱移到 C 柱上
- 将 A 柱上的第 n-1 个金盘移到 B 柱上
- 再将 C 柱上的 n-2 个金盘借助于 A 柱移到 B 柱上
- 然后将 A 柱上的最后一个金盘移到 C 柱上
- 再将 B 柱上的 n-1 金盘借助于 A 柱移到 C 柱上
是不是有点递归的意思了?
博主最近在学习 C 语言,所以试着用 C 来实现这个算法。代码如下
代码
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
#include <stdio.h>
/* 汉诺塔问题,输入金盘的数量 n ,输出将 n 个金盘从 A 柱(借助 B 柱)移动到 C 柱 的过程 */
int counter = 0; /* 初始化计数器 */
void move(char x, char y)
/* 输出一次移动 */
{
printf("\n%c-->%c", x, y);
counter++;
}
void hanoi(int n, char one, char two, char three)
/* 汉诺塔的递归算法 */
{
if (n == 1)
{
move(one, three);
}
else
{
hanoi(n-1, one, three, two);
move(one, three); /* 把 two 看作临时柱 */
hanoi(n-1, two, one, three);
}
}
int main()
{
for(;;) /* 实现多次模拟 */
{
int n;
printf("汉诺塔层数:");
scanf("%d", &n);
hanoi(n, 'A', 'B', 'C');
printf("\n\n移动次数:%d\n\n", counter);
counter = 0; /* 重置计数器 */
}
}
|
Python
当然也少不了Python啦
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
# 汉诺塔问题,输入金盘的数量 n ,输出将 n 个金盘从 A 柱(借助 B 柱)
# 移动到 C 柱 的过程
counter = 0 # 初始化计数器
def move(x, y):
'''输出一次移动'''
global counter
print(f"{x}-->{y}")
counter += 1
def hanoi(n, one, two, three):
'''汉诺塔的递归算法'''
if n == 1:
move(one, three)
else:
hanoi(n-1, one, three, two)
move(one, three)
hanoi(n-1, two, one, three)
while 1:
n = int(input("汉诺塔层数:"))
hanoi(n, 'A', 'B', 'C')
print(f"移动次数:{counter}\n")
counter = 0 # 重置计数器
|
结语
想起一句名言
算法 + 数据结构 = 程序
这是博主第一次真正认真学习算法,从此打开了新世界的大门(笑)
参考文献
[1]于延.C语言程序设计与实践[M].北京:清华大学出版社,2018(2019重印)
 用语言表述如下:
用语言表述如下: